4.2 Covariance, Correlation, Regression

When doing science, we often want to study the relation between two observables A and B. Most of the time, we want to foresee the future with partial information:

Can we foresee the behavior of A by knowing B? Or maybe the opposite? When one grows, what happens to the other?

We will use the following data to exemplify the following techniques:

• Birth Data Description
• Birth Data

1 Manual Experiment

The class will compile a list with the following information:

• Height
• Shoe size
• Number of brothers and sisters

We will make a graph with this information in Excel. What values seem to grow together? Which values seem to have no relation between them.

2 Correlation

Correlation is a measure of how two things behave similarly. For example:

• People’s height is positively correlated with their weight – that’s because a bigger height in general means a bigger weight.
• In a house, the amount of people is negatively correlated with the amount of space per person – that’s because the more people you have, the less space each one can have for themselves.

These behaviors can be seen in a graph. For example, look at this graph:

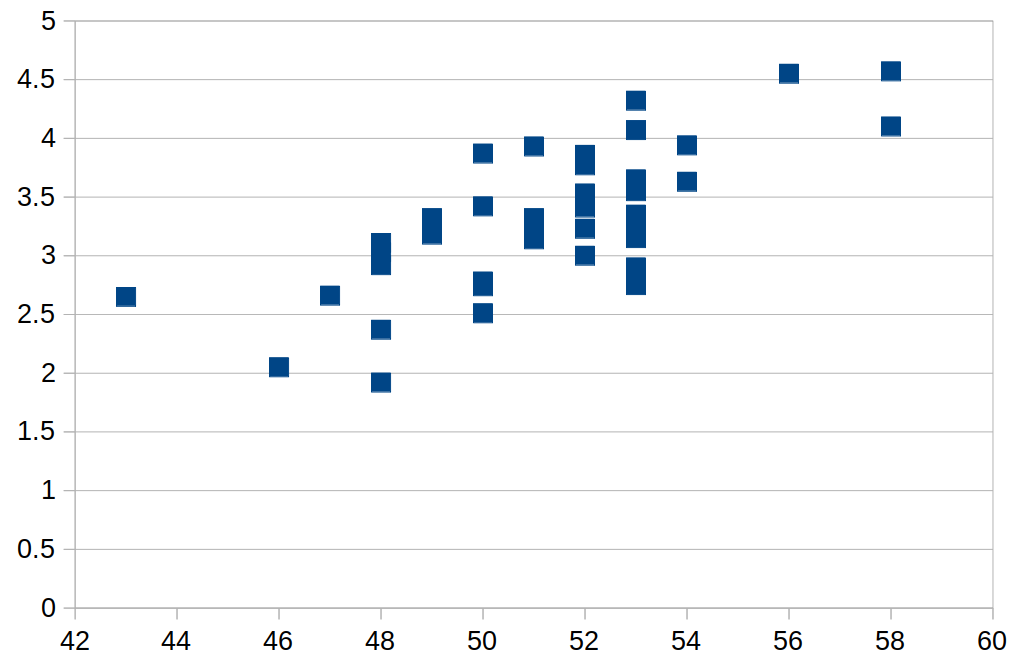
As we can see, the values tend to grow from the left to the right, together. This is the sign of a positive correlation.

Mathematically, there is a formula for correlation, which takes value from -1 up to 1. It goes from negatively correlated (-1), to uncorrelated (0) to positively correlated (1).

2.1 Formula

In order to calculate correlation, one needs sequences pairs of numbers. These sequences will be written x_1, ..., x_n and y_1, ..., y_n. Writing M_x for the average of x and M_y for the correlation of y, then the formula for correlation is:

r\_{xy} = \frac{\sum\_{i=1}^n (x_i-M_x) (y_i-M_y)}{\sqrt{\sum\_{i=1}^n (x_i-M_x)^2} \sqrt{\sum\_{i=1}^n (y_i - M_y)^2}}

2.2 In Excel

In Excel, the correlation between two data sets can be calculated using the CORREL(A1:A100,B1:B100) function, replacing the data ranges by the desired values.

2.3 Exercises

In the babies data set, there are many measurements. For any pair of measurements, we can:

• Create a X-Y scatter plot to visualize the data
• Analyze it, and try to infer if there is a positive, negative or no correlation.
• In a separate cell, measure the correlation using CORREL.

Some interesting pairs for doing it are:

• Size and weight
• Size and number of cigarettes smoked by the mother
• Weight and number of cigarettes smoked by the mother
• Size and father height
• Size and father years of education

3 Regression

In the section above we studied correlation. In some cases, such as weight and size, there is a very clear relation between the two variables. This deserves a question: can we model this relation with a straight line?

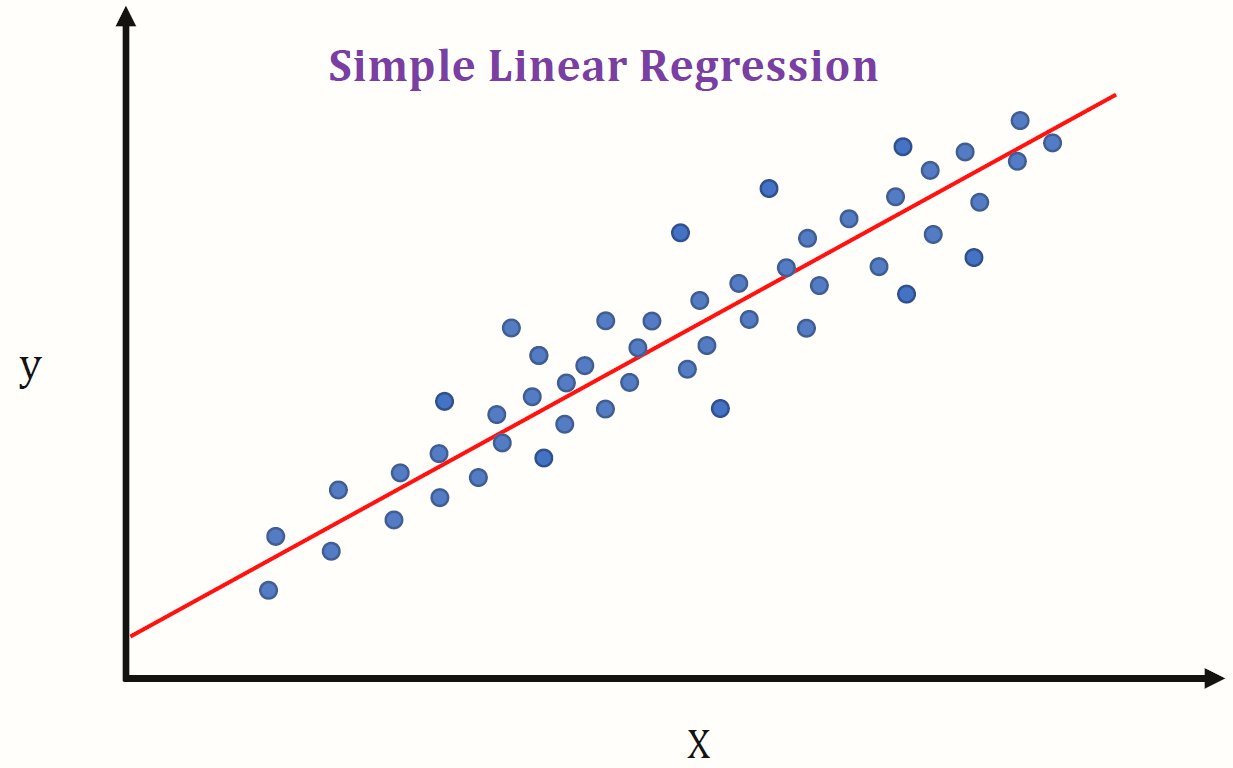
Look at the graph above: each blue dot has a coordinate (x,y). The straight line, is also composed by pairs of coordinates, such as the points, but its points follow a rule: y = \beta + \alpha x In this formula, there are two coefficients:

• \beta is the intersection coefficient: y = \beta when x = 0
• \alpha is the inclination coefficient: it measures the speed of increase or decrease of the variable

How should we draw this line? After all, we can draw any line in the graph, and it will be a model – but its quality can be better or worse, depending on the coefficients.

In order to choose the coefficients, we evaluate the error term:

The error term measures the difference between the measured value (one of the y_k values) and the value predicted by the model (calculated by \beta + \alpha x_k). The best model is the one which makes the error, measured by: \epsilon(\alpha,\beta) = \sum_{k = 1}^n (y_k - \beta - \alpha x_k)^2 as small as possible. The square (²) is there to make calculations easier.

If we use this criterion, we can calculate the regression coefficients as:

\beta = M_y − \alpha M_x

and

\alpha = r_{xy} \frac{\sigma_y}{\sigma_x}

where M represents the mean, r the regression coefficient, and \sigma the standard deviation.

3.1 Practice

Choose a pair of measurements. For this pair we will create a table with:

• Average of x (M_x)
• Average of y (M_y)
• Standard deviation of x (\sigma_x)
• Standard deviation of y (\sigma_y)
• Correlation of x and y (r_{xy})
• The \beta coefficient
• The \alpha coefficient
• The optimal \beta
• The optimal \alpha

Next to it, two columns:

• One with the prediction \beta + \alpha x
• Another with the error y − \beta − \alpha x

4 Control

Download the following:

• Control description: Russian or English
• Control spreadsheet: English

And follow the instructions. We will make rounds so all students can do the control by themselves.